Curve Stitching in the 21st Century
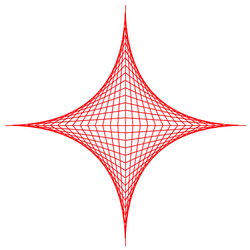
Wrapping up the school year, traveling in the Midwest, two retreats, and planning for the next year have kept me busy. Not too busy to explore math. In the spring, I started learning Javascript, a computer language to make webpages more interesting. I made the curve stitching on the left in less than ten lines of code! Javascript came in handy for making illustrations for a workshop on finding joy in mathematics. 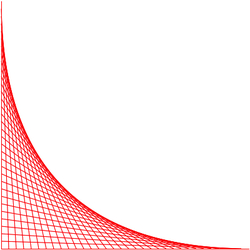 I began thinking about precalculus while making this half of a hyperbola. It struck me that, to some people, curves are no more than objects of fear rather than delight. Images linked to ugly formulas to be memorized, attached to definitions for bizarre words like conic section, asymptote, vertex, focal point, axis of symmetry, and reflection. Even people who had passed calculus in college did not see the connection between curve stitching and high- level mathematics. They remember memorizing facts divorced from concepts. Even in math, ideas must be clothed with facts as they occur.
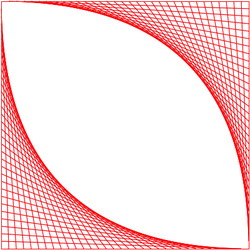 Isn't this cat's eye lovely?
To make this, I reflected the half hyperbole along a line between the corners of the eye. I resurrected foggy notions of the Cartesian coordinate system (x-axis versus y-axis). Through trial and error — math people never do things correctly the first time — I figured out that swapping the x and y values. It was tricky. I couldn't apply precalculus rules for transformation since Javascript grids are different. The origin (0, 0) is the upper left corner of the square and (400, 400) is the lower right corner. I had to play!
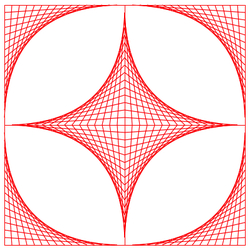
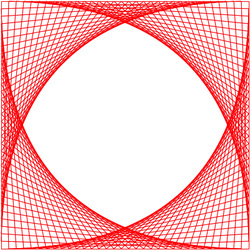 Then, I went curve stitching crazy! I made a fancy frame with two cat's eyes with lines of symmetry that make right angles (or form perpendicular lines). Again, this was an exercise in trial and error. It took me even longer to figure out I needed to swap x and y at one point, instead of both.
I know! Too many facts. Playing with curves invites ideas. Putting them together differently leads to beautiful designs. Figuring out how to code them has caused deep thinking. Curve stitching inspires wonder and encourages questions to be asked and answered years before taking precalculus.
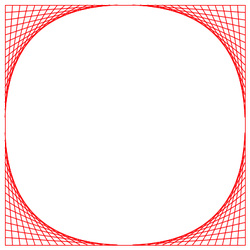 I wanted to write Javascript for a cross. I randomly tried one variation after another and wasted an hour making a mess! Then, I took a break and started over.
I began to think. What if I made a frame that looks like an old-fashioned television screen?
The four pieces (one per corner) would be half the size of those on the fancy frame. This step points to a key element of problem-solving: break the process down into smaller steps and conquer the problem one step at a time.
 The final step is simply a matter of moving pieces vertically and horizontally. Look at the upper left corner of the television screen. Imagine where that piece belongs in the cross IF you don't rotate it or flip it. You put your finger in the corner of the piece. You push it halfway down the television screen and halfway across. Put your finger on the image on your computer screen if you must. Can you see it?
If not, make a quick sketch of the television screen and cut it out along the edge. Cut it into four equal pieces. Treat the pieces like manipulatives and make a cross by moving them.
 The final design places the cross inside the television screen. In Javascript, I simply put the lines of code for eight pieces in the same loop. What looks complicated was easy!
Then, I realized something! When tutoring someone in precalculs, I looked up how to change a formula to shift the curve to another point. This tangible process helped me see that all you need to do is adding a positive or negative number to the original coordinates. Reflection requires the x and y coordinates to swap places. From now on, all I need to do is recall curve stitching!
Curve stitching is a lot of fun. My friend Bobby Jo, a homeschooler who introduced me to paper sloyd, captioned a picture of my original Valentine cards as “Sloyd marries curve stitching" Math + Handcraft heaven.How do you start? Here is a quick tour. First read my post, Curve Stitching Roundup, an orderly review of what curve stitching is, who invented it, and interesting variations. Since that post, I've added a few elaborations: six-petal flower, picture frame, valentine I, valentine II, and valentine III.
Sloyd Pinwheels
A Captain Idea for us, — Education is the Science of Relations. — A child should be brought up to have relations of force with earth and water, should run and ride, swim and skate, lift and carry; should know texture, and work in material; should know by name, and where and how they live at any rate, the things of the earth about him, its birds and beasts and creeping things, its herbs and trees; should be in touch with the literature, art and thought of the past and the present. ~ Charlotte Mason
 I've had such a busy spring that paper sloyd with Pamela has taken a back seat. Fortunately, I taught paper sloyd to the students at our school for the last term of handwork. I am so delighted to report that Pamela can follow directions in a large group and work independently! This is major progress for her! The students at our school made the first four projects from the paper sloyd handbook.
 To some, making paper projects seems like a waste of time when we could spend that half-hour (elementary class) or hour (primary class) pouring more knowledge into their heads. Think back to when you were in school. How many of you do anything “productive” much less learn anything “important” in the last hour before the weekend starts — especially after spring fever has infected the brain?
I am now convinced that kids today need handwork more than ever.
 I've seen kids struggle to use tools (scissors, rulers, glue, tape, needle and thread, etc.) at older ages than expected. I've seen older students be unsure of how to make props for Shakespeare scenes. The kids in our church afterschool program beg for clay every week! It's like they're starving.
Children gravitate toward screens during their free time. If we find educational games that teach them something academic, we feel a little better about it. Families are so busy making ends meet that we are too exhausted a little bit of mess into the home for handwork.
 Schools under the gauntlet of boosting standardized test scores squeeze it out as well. A friend of mine remarked that she is seeing more and more typical students referred for occupational therapy because they cannot use their hands well. Temple Grandin outlines many reasons why hands-on classes need a comeback. Kids who struggle with academics look forward to handwork. It teaches them problem solving, careful execution, improvisation, etc.
We found the opportunities to problem solve. The first time we made pinwheels we made the mistake of using cardstock. One student in the next class decided to make a pinwheel in cardstock and another with colored copy paper. The students learned really quickly that too much glue ruins the paper. They figured out how to tilt the pinwheel just so and blow in the perfect spot to make it spin.Plus, I inserted proper math terms into the conversation. I really despise the hamburger versus hotdog terms for portrait and landscape. Why? Because when you use real computer software to set up an image or document, they use the latter terms.We had a blast making our pinwheels!
The Thrill of Discovery
Education is the Science of Relations -- He should feel the thrill, not from mere contiguity, but because he has with the past the relationship of living pulsing thought; and, if blood be thicker than water, thought is more quickening than blood. He must have a living relationship with the present, its historic movement, its science, literature, art, social needs and aspirations. In fact, he must have a wide outlook, intimate relations all round. ~ Charlotte Mason
That sounds well and good until you get to math. Geeks are the rare birds whose blood quickens with delight over math. The tricky part is helping others find that thrill.
I've been helping a student struggling in a dry geometry class taught with an eye toward memorizing theorems and lacking in hands-on exploration and connections to history much less the real world. I chose Jacob's Geometry for our text because it puts students in touch “with the past" and develops “the relationship of living pulsing thought." In our conversations about big ideas in geometry, the student's eyes have opened to see connections she has never noticed before. She asks good questions. She told me the other day, “I'm starting to appreciate geometry for the first time in my life."
While studying vocabulary for polygons, we came up with words that begin with something like oct. In Spanish, ocho means eight. An octopus has eight legs, while an octave has eight notes. But, what about October? October used to be the eighth month until a reworking of the calendar added July, named for Julius Caesar, and August, named for his nephew and successor, Augustus.
I believe that vocabulary words are best learned in context of living ideas and through application, not from writing definitions to be memorized. My opinion was validated this week. My student said she shared the meaning of October with her mother who'd never made this connection before. She remembered the meaning of vocabulary words on her test.
One lesson from this living math textbook sparked a conversation about sundials. A teacher brought hers to school and we observed how sundials work firsthand. My student gushed,
“I'd never thought about how people told time before clocks were invented." Now, she is experiencing a wider outlook.
That lowly sundial lead to rapture for one of our autistic students. I promised to show him how people told time before clocks were invented. He is very observant, so I asked him what he noticed. “There's a shadow." “It's pointing to some letters." “I see a lot of letters." I briefly explained that people used sundials as clocks in the days when Jesus walked the earth.
“Really?"“Yes, really!" I added, “Those letters are numbers. They are called Roman numerals." Then we started at VI, the first numeral, and worked our way around the sundial until VI in the evening. He seemed a tad bored.
Rather than hit him with comprehension questions, I took a circuitous route. I asked, “Have you ever seen numbers like these before?" Then, I paused and waited for him to think. He studied the sundial for a minute or two.
Suddenly, he gasped. The kind of gasp that told me he had just made a vital connection.
“MRS. TAMMY! THOSE ARE STAR WARS NUMBERS!" Rapture poured over him. “Can I get some paper? I need to write this down in date order."
This young lad who typically approaches copywork with reluctance and resists doing math sat down and wrote down the hallowed list of the Star Wars movies, in date order, with punctuation, with episode numbers recorded in Arabic numbers and Roman numerals. He was so joyful he headed to a large stack of kids' magazine donated to the school a few months ago and found the one with all six episodes in date order. We followed up his list writing with some Roman numeral matching cards I'd made last summer. He was so excited about his discovery — for he owned this one — he exclaimed, “I cannot wait to tell my dad about the Star Wars numbers."
Gimme Pi!
When my children were little, we celebrated advent by singing Christmas carols around a lit advent wreath. Afterwards, I served a treat. My son, four years old at the time, didn't quite have the knack of advent. He requested songs like “Old MacDonald Had a Farm." Once he'd had his fill of songs, he punctuated our singing with “Gimme pie!" Every time I think of Pi Day, the cry “Gimme pi!" rings in my ears.
Last Friday, I completely missed out on Pi Day. A friend invited us over for some chicken pot pie and caramel pumpkin pie. I left school after the nature walk and spent the rest of the day and night in bed with a bad head cold. But, that's okay. The Pi Day that really counts is next year, specifically 3/14/15 9:26:53 a.m.
What is pi? Pi is a ratio of a circle's circumference (C) and diameter (d): π = C/d.
Most people say that it's a number used to find the area of a circle. Pi is more than that!
First, it's constant. By constant, I mean it's a number that's true for every circle in existence. Regardless of the size of the circle, pi is always pi. It never varies. It never changes.
Second, it's non-terminating. By non-terminating, I mean it's without end. Pi just goes on and on and on, one digit after another with no end in sight.
Third, it's non-repeating. By non-repeating, I mean that, although it goes on forever, pi never repeats a pattern of digits. No matter how far you take pi, you'll never see it repeat itself in the sequence of digits.
Fourth, it's irrational. By irrational, I mean that you cannot calculate pi by dividing one integer by another. The ratio 22/7 isn't pi. It's an approximation of pi that makes number crunching easier if you've lost your calculator.
I love the paradoxes of pi.
Pi is constant and yet it never repeats.
Pi is irrational, but it's also a ratio.
Here is what I like most about pi. Some infinite series converge to pi.
Huh?
This is an infinite series.
π = 3 + 4/(2 x 3 x 4) - 4/(4 x 5 x 6) + 4/(6 x 7 x 8) - 4/(8 x 9 x 10) + 4/(10 x 11 x 12) - + ...
Do you see how the pattern works: the sign of the term alternates between positive (+) and negative (-). The number 4 is always in the numerator (the top part of the fraction), so the next term will subtract 4 over something. The denominator takes the third number of the product in the denominator of the last term (12) and multiplies it by the next two consecutive integers: 13 and 14. Thus, the next term will be: - 4/(12 x 13 x 14).
If you go term by term, you can see how this series gets close to pi as you add more terms.
First Term:
π ≈ 3
Second Term:
π ≈ 3 + 4/(2 x 3 x 4) = 3 + ¹⁄₆ = 3 ¹⁄₆= 3.1666...
Third Term:
π ≈ 3 ¹⁄₆ - 4/(4 x 5 x 6) = 3 ¹⁄₆ - ¹⁄₃₀ = 3 ²⁄₁₅ = 3.1333...
Fourth Term:
π ≈ 3 ²⁄₁₅ + 4/(6 x 7 x 8) = 3 ²⁄₁₅ + ¹⁄₈₄ = 3 ⁶¹⁄₄₂₀ = 3.14523809523809....
I created a spreadsheet to make these calculations because they're tedious.
At the 1st term, the series converges to the ones place of pi: 3.166666666...
At the 2nd term, the series converges to the tenths place of pi: 3.133333333...
At the 6th term, the series converges to the hundredths place of pi : 3.14271284271...
At the 9th term, the series converges to the thousandths place of pi: 3.141254823...
At the 33rd term, the series converges to the ten-thousandths place of pi: 3.141585704...
At the 46th term, the series converges to the hundred-thousandths place of pi: 3.141595220...
At the 89th term, the series converges to the millionths place of pi: 3.141592299...
At the 175th term, the series converges to the ten-millionths place of pi: 3.141592606...
At the 412th term, the series converges to the hundred-millionths place of pi: 3.141592657...
At the 849th term, the series converges to the billionths place of pi: 3.141592653...
Do you see why Pi Day 2015 is a big deal?
π ≈ 3.141592653
3/14/15 9:26:53 a.m.
You might find a picture of this process interesting. The chart shows how the series dances above and below pi until it converges according to what the naked eye sees.
Pricey Manipulatives? Think Again!
March has roared in like a lion her between the chilly weather, a short trip to Louisiana for a wedding, an open house, and succumbing to a nasty head cold (probably due to the aforementioned whirlwind). Fortunately, you've had time to toy with Pascal's Triangle. I hope you've moved ahead because it means you're learning to play with math! If not, here is the next installment.

 Varying your choice of manipulatives might be better than sticking with the same old thing. Studying in two different rooms helps encode memory more firmly than studying in the same spot. “The brain makes subtle associations between what it is studying and the background sensations it has at the time, the authors say, regardless of whether those perceptions are conscious. It colors the terms of the Versailles Treaty with the wasted fluorescent glow of the dorm study room, say; or the elements of the Marshall Plan with the jade — curtain shade of the willow tree in the backyard. Forcing the brain to make multiple associations with the same material may, in effect, give that information more neural scaffolding."
 How can we use these? Well, pick a two-digit number: 84. The gray box represents the ones digit, which is 4. The white towers represent the tens digit 8. To make the number 84, you'll need ten towers and one gray box. To make it easier, I'll annotate numbers on the manips. You can simply add up the numbers to see that this equals the number 84.
 The next step is to reorganize manips in a way to get to your goal: adding the tens and ones digits (8 and 4). Nine towers are left and can be rearranged into three groups. Anything that can be divided into three groups is divisible by three as you can see in the next picture. Clearly, the set of white towers is divisible by 3.
 If adding one white tower (the tens digit) and one gray box (the ones digit) yields a number divisible by 3, then the original number (84) is divisible by 3. If the sum (8 + 4) isn't divisible by 3, then neither is the number (84). Try this out with any two digit number and you will see that regardless of number, you end up with nine white towers in one pile and a white tower and gray box in the other.
So, what would happen if the labels fell off the manipulatives?
They would represent any generic two-digit number.
After enough play for this to make sense, the next level of abstraction would be to draw what you just did. A circle representing tens digit (the white towers) and a square, the gray box (ones digit). Try drawing and filling in the squares with the tens digit and the circles with the ones digit until it makes sense. Then see what happens when you don't fill in the blanks. The same process happens regardless of the tens digit and the ones digit.
The final leg of the journey to abstract land would be to represent the two-digit number, yx, where y is the tens digit and x is the ones digit. You've been doing the math all along with objects and drawings. The expressions are simply a way to represent what you've already been doing algebraically. If reading the final line of expressions makes your head swim, try going through the process with manips and by drawing first. DON'T JUST READ! PLAY!
| ❍❍❍❍❍❍❍❍❍❍❍ ❏ 10y + x
| ❏❏❏❏❏❏❏❏❏ ❏❍ 9y + (y+x)
| ❏❏❏ ❏❏❏ ❏❏❏ ❏❍ 3(3y) + (y+x)
| Manipulatives get confusing with large numbers such as a three-digit number. When my kids studied place value with Making Math Meaningful, they used toothpicks. You could try some colored ones: there are 100 plain toothpicks for the hundreds digit, 10 blue toothpicks for the tens digit, and 1 red toothpick for the ones digit. Again, it doesn't matter what the digits are; the process is the same. Pull one toothpick from each bundle to add them, leaving 99 plain and 9 blue toothpicks. Since you can group both colors into three equal groups, they are divisible by 3. If the sum of the digits is divisible by 3, then so is the actual number.
Going abstract, let zyx be the three-digit number in which z is the hundreds digit, y is the tens digit, and x is the ones digit. You can see what happens below each picture.
| 100z + 10y + x
| 99z + 9y + (z + y + x)
| 3(33z) + 3(3y) + (z + y +x)
| For four-digit numbers and beyond, Making Math Meaningful suggested paper grids. Hopefully, you'll follow the logic if you've tried manips up until this point. There are 1,000 purple squares for the thousands digit, 100 red squares for the hundreds digit, 10 blue squares for the tens digit, and 1 red toothpick for the ones digit. Pull one toothpick from each bundle to add them, leaving 99 plain and 9 blue toothpicks and divide into three groups.
Going abstract, let azyx be the four-digit number in which a is the thousands digit, z is the hundreds digit, y is the tens digit, and x is the ones digit. You can see what happens below each picture. | 1000a + 100z + 10y + x
| 999a + 99z + 9y + (a + z + y + x)
| 3(333a) + 3(33z) + 3(3y) + (a + z + y + x)
|
|